FrontierMath explained without Mathematics
A Simplified Q&A for ML Practitioners and Curious Minds
What is FrontierMath? Why do we even need it?
FrontierMath is a new dataset of maths problems and a benchmark for AI model training containing never-before-seen math problems that force models to demonstrate real reasoning abilities instead of relying on memorized patterns. It contains a wide variety of contemporary mathematics topics, including those that are at the research level, in contrast to the majority of extant math benchmarks. These problems have been provided by more than 60 mathematicians including 14 people who were winners of IMO and one person won a Field’s medal (Nobel prize equivalent in mathematics). So, it would be safe to assume that most of these problems would be hard. Although solving benchmark problems is not entirely equivalent to creating original proofs, but authors in the paper believe that FrontierMath is a significant step to fully automate the mathematics research. We need FrontierMath benchmark due to the following main reasons:
1. To Test Genuine Understanding (Not Memorization)
Most existing math benchmarks contain problems that have been around a while. Large Language Models before OpenAI’s O3, have been trained on MBPP (Most Basic Programming Problems) for coding tasks. Similarly for Mathematical problems, a large corpus of mathematical problems and proofs are provided to a large neural network with parameters ranging from billions to ~trillion params. This large network and large corpus together becomes a “Problem-Solution Template” for pattern matching. So in a way these networks have indirectly “seen” the patterns and they recall answers utilizing their Problem-Solution Templates memory, rather than truly reason them through.
2. To Push the Limits of AI Thinking
Many standard math challenges are too narrow. They check whether a model knows this or that formula. They verify whether a model is familiar with a particular formula. FrontierMath's problems are a memetic dataset of problems that emulate the thought processes of accomplished mathematicians in their respective fields, including number theory, combinatorial optimization, np-complete problems, and np-hard problems. This memetic dataset tries to link different branches of mathematics and allows the neural networks to mimic the way real mathematicians tackle uncharted territory. This may still not be the pure human-level mathematical ingenuity but, it attempts to roughly approximate it.
3. To Highlight Where AI Struggles
Researchers can discover where AI reasoning is lacking, such as in logic, issue decomposition, or long-term planning, by observing when even the best AI models make mistakes. FrontierMath does a good job at drawing attention to holes in the AI's "thought process."
4. To Spur Progress
We all chase targets in our lifes. Model Benchmarks are no different. They create targets for AI researchers to aim for. When a model solves, say, only 2% of the problems, it motivates the community to develop better techniques. Every improvement is tested against these difficult puzzles, pushing AI steadily forward.
5. To Safeguard Against ‘Data Contamination’
Since FrontierMath’s problems are new, they’re not floating around the internet or in textbooks. This avoids the problem of AI having “seen” half the test set in its training data. Thus, we get a cleaner, more honest measure of how an AI performs when faced with truly novel challenges.
What types of Mathematical problems are utilized in the benchmark?
I am providing a simplified, overview of the three sample problems featured in the paper:
Artin’s Primitive Root Conjecture:
It is much like a spinning top. If we imagine a spinning top that we give a gentle push. It whirls around and eventually lands in some position. Now, suppose there's a special kind of top so magical that, no matter how many times or how hard you spin it, it {always} ends up in a completely new position. In mathematical terms, Artin’s Primitive Root Conjecture is all about whether certain numbers (like 2 or 3) can, when multiplied over and over under a prime, hit {every possible remainder} exactly once before coming back to 1. If this is true for infinitely many primes, then the top is truly “magic”. Basically, it never repeats a position too soon.
Find the degree 19 polynomial:
Picture an AI team building a workflow that needs to handle different kinds of data such as like images, text, and audio. Each type of data has its own special “door” in the system. Whenever a new data type shows up, it triggers a hidden path (like opening a secret door) that leads to a completely new sub pipeline.
Now compare this to constructing a degree 19 polynomial with special rules such as being monic, odd, and having a particular linear coefficient. It’s like designing that workflow so it splits into multiple distinct “sections.” When you run a specific test (like plugging in x = 19), you’re checking which sub pipeline you end up in. The real challenge is balancing all those special rules while still allowing the system to branch in just the right ways—like building a branching workflow that remains well-organized even as it grows more complex.
Prime field continuous extensions
Imagine you are in an AI team that has spent months training a model on familiar hardware on self-hosted HPC cluster. Suddenly, your boss tells you, “We need to deploy our system in a high-security data center that uses unusual hardware where numbers behave differently.” This new hardware has rules unlike anything in your normal environment: standard arithmetic doesn’t work the same way, and “distance” between numbers is measured in a peculiar fashion.
In mathematical terms, that’s similar to the p-adic setting. We have a sequence (like a data stream) defined by a big recurrence formula. The question is which prime will make it possible for that sequence to “plug in” and work smoothly in this exotic environment. Finding such a prime is like discovering the perfect key or adapter so your AI model doesn’t break under the center’s strange constraints. If you pick the wrong prime, it’s as if your model’s updates will keep getting scrambled no continuous, stable behavior. But the right prime brings everything together, letting the model function seamlessly in this “quirky” new world.
How FrontierMath Checks a Large Language Neural Network’s Work Work?
Here’s a simple explanation of what happens in the above workflow:
The Network Generates an Answer
The large language neural network doesn’t just provide a number or statement. Instead, it writes a small piece of code that computes its proposed answer. For example, it might produce code that calculates a pair of integers (x,y)(x, y)(x,y) to satisfy a particular equation.Answer is Stored
That code then stores its final result (like (8,3)(8, 3)(8,3) or (2,2)(2, 2)(2,2)) in a file, often using Python’s “pickle” format. This file is the network’s official answer.Verification Script Checks the Answer
A separate “verification script” loads the stored answer and automatically checks its validity. If the task says, “Find integers xxx and yyy such that x2−7y2=1x^2 - 7y^2 = 1x2−7y2=1,” the script just plugs in xxx and yyy.If the equation holds (e.g., 82−7×32=18^2 - 7 \times 3^2 = 182−7×32=1), the script marks the answer correct.
If it doesn’t, the script marks it incorrect.
All the algebra is performed using SymPy library.
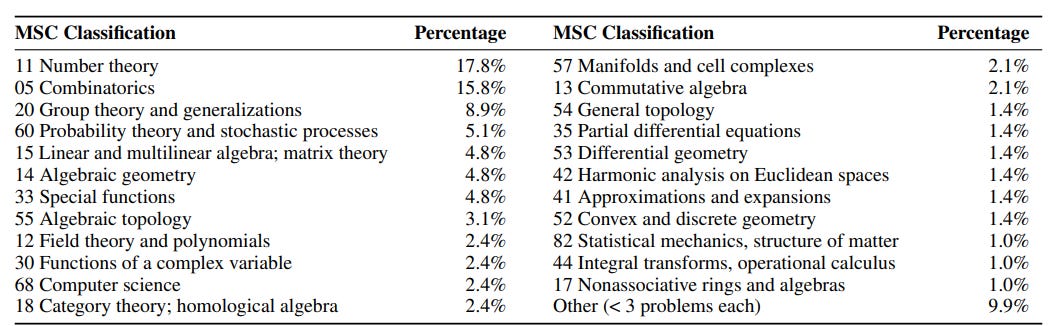
What is the Mathematics Subject Classification (MSC)?
The Mathematics Subject Classification (MSC) is a system used by mathematicians worldwide to categorize research papers, books, and problems based on their field of study. Each code corresponds to a distinct branch or sub-branch of mathematics—like number theory, combinatorics, or algebraic geometry. This helps researchers (and AI) quickly identify the main subject area of a mathematical work.
FrontierMath authos assign at least one MSC 2020 code to each problem to indicate its primary topic. The percentages you see represent how frequently each MSC code appears across the entire dataset. Essentially, if you slice up the collection of problems by mathematical “genre,” each slice’s percentage indicates how large a presence that particular area of math has within FrontierMath. This distribution also shows whether the dataset is broadly covering many areas (like number theory, analysis, etc.) or if it focuses heavily on just a few.
Following is the composition listed in the paper:
What are the main shortcomings of the benchmark?
Exclusion of Proof-Writing and Open-Ended Exploration: How can someone do mathematics research without writing proofs and open-ended exploration. Ramanujan had a kind of “mathematical sixth sense” that he invariably gave correct answers without proof. But, we know that LLMs are not Ramanujam!! 🤷♂️
Potential for Data Contamination: Although the study aims to use exclusively novel problems to prevent data contamination, I suspect that O1 has already been trained on it. So, the O3 model may not entirely reason out on the FrontierMath benchmark. ❌ It is also possible that future models may have a peek into the kind of problems used in the dataset and be gamed to memorize the patterns instead of reasoning them.
Difficulty Assessment Limitations: While the peer-review process aims to validate difficulty ratings, discrepancies between authors’ and reviewers’ assessments may still exist, which could affect their accuracy.
Noise from Errors: The study acknowledges that errors in question statements or computational mistakes in solutions are common, particularly among new authors, which could introduce noise into the benchmark.
Some Reflections:
First, watch this video..
While all this progress happens in Benchmarks and automated Maths research, as researchers we should not forget that Proofs are not purely objective. At best, they are agreements within the mathematical community, accepted based on verification by peers from various perspectives.
Richard Feynman once remarked that scientific proofs begin with a guess, followed by computing the consequences of that guess, and then comparing the results to observations in nature. If the results align, we consider the phenomenon explained. However, mathematics goes beyond being a purely logical endeavor—it is an iterative process of formulating and refining guesses, carried out by countless researchers through repeated iterations and corrections over time.
Capturing the vast dimensions of mathematics within a sparse benchmark is inherently reductive, akin to how sparse autoencoders distill only the most salient features while leaving much of the detail behind. For this reason, as researchers and machine learning practitioners, we must approach such benchmarks with healthy skepticism, no matter how reputable their creators may be. They can only provide a glimpse into the field, not its full complexity.
About the Author
Bhaskar Tripathi is a leading open source contributor and creator of several popular open-source libraries on GitHub such as pdfGPT, text2diagram, sanitized gray wolf algorithm, tripathi-sharma low discrepancy sequence, TypeTruth AI Text Detector, HypothesisHub, Improved-CEEMDAN among many others. He holds a PhD and several international patents and publications in the area of Financial Mathematics and Computational Finance.
Personal Website: https://www.bhaskartripathi.com
Linkedin : https://www.linkedin.com/in/bhaskartripathi/
Google Scholar: Click Here